Polynomial Fitting in C program

Okay, so here I am sharing a code for fitting a polynomial to a given set of data-points using the Least Squares Approximation Method(Wikipedia).

Let’s say we have 

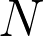
 data-point pairs and we are trying to fit them using a polynomial of degree 

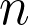
. If N=n+1 then the polynomial will pass exactly through each point and it will correspond to the interpolating polynomial that I wrote about earlier.

Let’s say the polynomial we are using is given as:

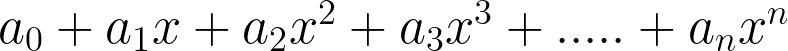
with errors given by

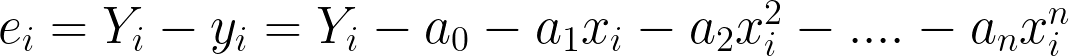
Here, we are using 

 to represent the observed data-points corresponding to 

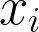
. We now minimize the following quantity

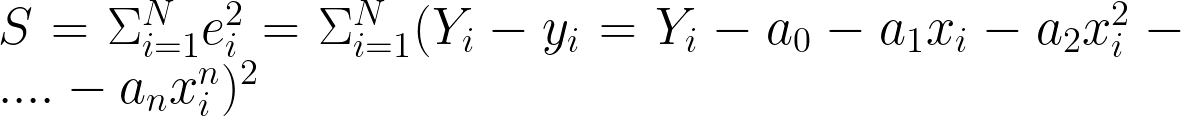
At the minimum all the partial derivatives with respect to the coefficients will vanish. This will give us the following 

 equations:

 

.
.
.

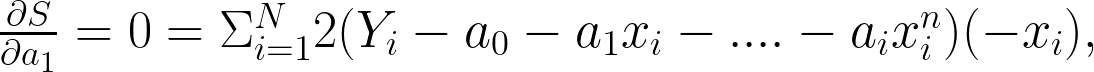
Dividing each by -2 and rearranging gives the 

 normal equations to be solved simultaneously:

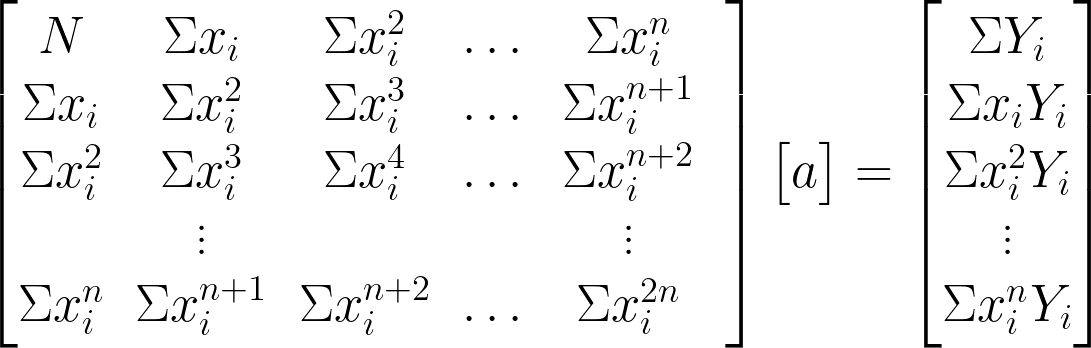
where 

 and 

 are the data-points entered by the user and 

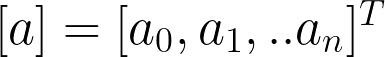
 which are the required coefficients.

So we just need to build up the above system of equations and then solve it using Gaussian elimination to get the coefficients.

The following program illustrates the process.

 

/******************************************************
*************Chi-square fitting**************
Polynomial Fitting
******************************************************/
#include<stdio.h>
#include<math.h>
/*******
 Function that performs Gauss-Elimination and returns the Upper triangular matrix and solution of equations:
There are two options to do this in C.
1. Pass the augmented matrix (a) as the parameter, and calculate and store the upperTriangular(Gauss-Eliminated Matrix) in it.
2. Use malloc and make the function of pointer type and return the pointer.
This program uses the first option.
********/
void gaussEliminationLS(int m, int n, double a[m][n], double x[n-1]){
    int i,j,k;
    for(i=0;i<m-1;i++){
        //Partial Pivoting
        for(k=i+1;k<m;k++){
            //If diagonal element(absolute vallue) is smaller than any of the terms below it
            if(fabs(a[i][i])<fabs(a[k][i])){
                //Swap the rows
                for(j=0;j<n;j++){                
                    double temp;
                    temp=a[i][j];
                    a[i][j]=a[k][j];
                    a[k][j]=temp;
                }
            }
        }
        //Begin Gauss Elimination
        for(k=i+1;k<m;k++){
            double  term=a[k][i]/ a[i][i];
            for(j=0;j<n;j++){
                a[k][j]=a[k][j]-term*a[i][j];
            }
        }
         
    }
    //Begin Back-substitution
    for(i=m-1;i>=0;i--){
        x[i]=a[i][n-1];
        for(j=i+1;j<n-1;j++){
            x[i]=x[i]-a[i][j]*x[j];
        }
        x[i]=x[i]/a[i][i];
    }
             
}
/*******
Function that prints the elements of a matrix row-wise
Parameters: rows(m),columns(n),matrix[m][n] 
*******/
void printMatrix(int m, int n, double matrix[m][n]){
    int i,j;
    for(i=0;i<m;i++){
        for(j=0;j<n;j++){
            printf("%lf\t",matrix[i][j]);
        }
        printf("\n");
    } 
}
main(){
    //no. of data-points
    int N;  
    //degree of polynomial
    int n;  
    printf("Enter the no. of data-points:\n");
    scanf("%d",&N);
    //arrays to store the c and y-axis data-points
    double x[N], y[N];  
    printf("Enter the x-axis values:\n");
    int i,j;
    for(i=0;i<N;i++){
        scanf("%lf",&x[i]);
    }
    printf("Enter the y-axis values:\n");
    for(i=0;i<N;i++){
        scanf("%lf",&y[i]);
    }
    printf("Enter the degree of polynomial to be used:\n");
    scanf("%d",&n);
    // an array of size 2*n+1 for storing N, Sig xi, Sig xi^2, ...., etc. which are the independent components of the normal matrix
    double X[2*n+1];  
    for(i=0;i<=2*n;i++){
        X[i]=0;
        for(j=0;j<N;j++){
            X[i]=X[i]+pow(x[j],i);
        }
    }
    //the normal augmented matrix
    double B[n+1][n+2];  
    // rhs
    double Y[n+1];      
    for(i=0;i<=n;i++){
        Y[i]=0;
        for(j=0;j<N;j++){
            Y[i]=Y[i]+pow(x[j],i)*y[j];
        }
    }
    for(i=0;i<=n;i++){
        for(j=0;j<=n;j++){
            B[i][j]=X[i+j]; 
        }
    }
    for(i=0;i<=n;i++){
        B[i][n+1]=Y[i];
    }
    double A[n+1];
    printf("The polynomial fit is given by the equation:\n");
    printMatrix(n+1,n+2,B);
    gaussEliminationLS(n+1,n+2,B,A);
    for(i=0;i<=n;i++){
        printf("%lfx^%d+",A[i],i);
    }
     
}

 

출처 : https://www.bragitoff.com/2018/06/polynomial-fitting-c-program/